无重复字符的最长子串:破解无重复字符子串的终极算法
引言:字符串中的寻宝游戏
如果把字符串比作一条热闹的商业街,每个字符都是一家特色店铺,那寻找「无重复字符的最长子串」就像在这条街上找一段没有连锁加盟店的最长街区。这个问题看似简单,却藏着算法世界里的「效率密码」——从青铜程序员的「地毯式搜索」到王者工程师的「精准打击」,折射的正是算法优化的终极哲学:用最少的资源,办最多的事。
解法等级划分
青铜解法:暴力拆迁队的野蛮搜索
直观思路:把所有可能的子串都揪出来检查一遍,像拆迁队一样挨家挨户敲门问:「你们家有重复的吗?」
func lengthOfLongestSubstring(s string) int {
// 处理空字符串边界情况
if len(s) == 0 {
return 0
}
// 记录最长子串长度
maxLenth := 1
// 记录当前子串长度
currentLenth := 1
// 外层循环:以每个字符为起始位置查找最长子串
for index, char := range s {
// 存储已出现的字符及其索引,用于快速检测重复
dataMap := make(map[rune]int)
dataMap[char] = index
currentLenth = 1
// 内层循环:从起始位置后一位开始扩展子串
for j, v := range s {
// 跳过起始位置之前的字符
if index >= j {
continue
}
// 检测到重复字符,终止当前子串扩展
if _, exist := dataMap[v]; exist {
break
} else {
// 无重复则延长当前子串并更新最大长度
currentLenth++
if currentLenth >= maxLenth {
maxLenth = currentLenth
}
}
// 记录当前字符位置
dataMap[v] = j
}
}
return maxLenth
}
提交结果
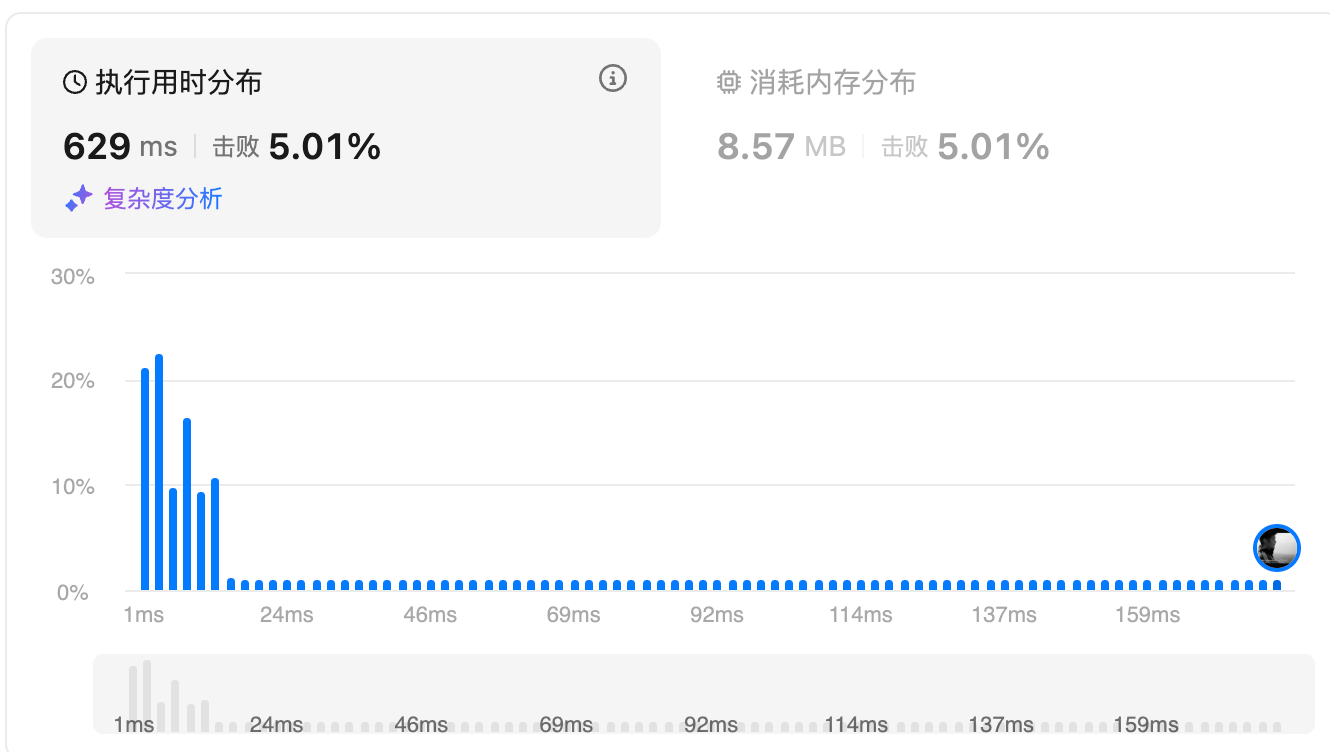
复杂度分析:
- 时间复杂度:双层循环结构,外层循环遍历每个字符作为起始点 (O(n)), 内层循环扩展子串 (最坏情况O(n)),像兔子在跑步机上跑步——忙得团团转却没前进多少
- 空间复杂度:O(min(m,n)) - m是字符集大小,哈希表最多存储不重复的字符
青铜程序员的痛点:当字符串长度达到10⁴级别,这个算法就会像老旧电脑运行大型游戏一样——直接卡死,能实现需求,但是数据量大的时候,直接卡死。
白银解法:哈希表+滑动窗口的雏形
优化思路:用哈希表记录字符最后出现的位置,像给每个字符发一张「门禁卡」,记录它们最近一次出现的时间。
func lengthOfLongestSubstring(s string) int {
n := len(s)
maxLen := 0
lastOccurred := make(map[byte]int) // 字符 -> 最后出现的索引
left := 0 // 滑动窗口左边界
for right := 0; right < n; right++ {
char := s[right]
// 如果字符已出现且在当前窗口内,则移动左指针到重复字符的下一位
if pos, exists := lastOccurred[char]; exists && pos >= left {
left = pos + 1
}
// 更新最大长度
currentLen := right - left + 1
if currentLen > maxLen {
maxLen = currentLen
}
// 更新字符最后出现的位置
lastOccurred[char] = right
}
return maxLen
}
提交结果
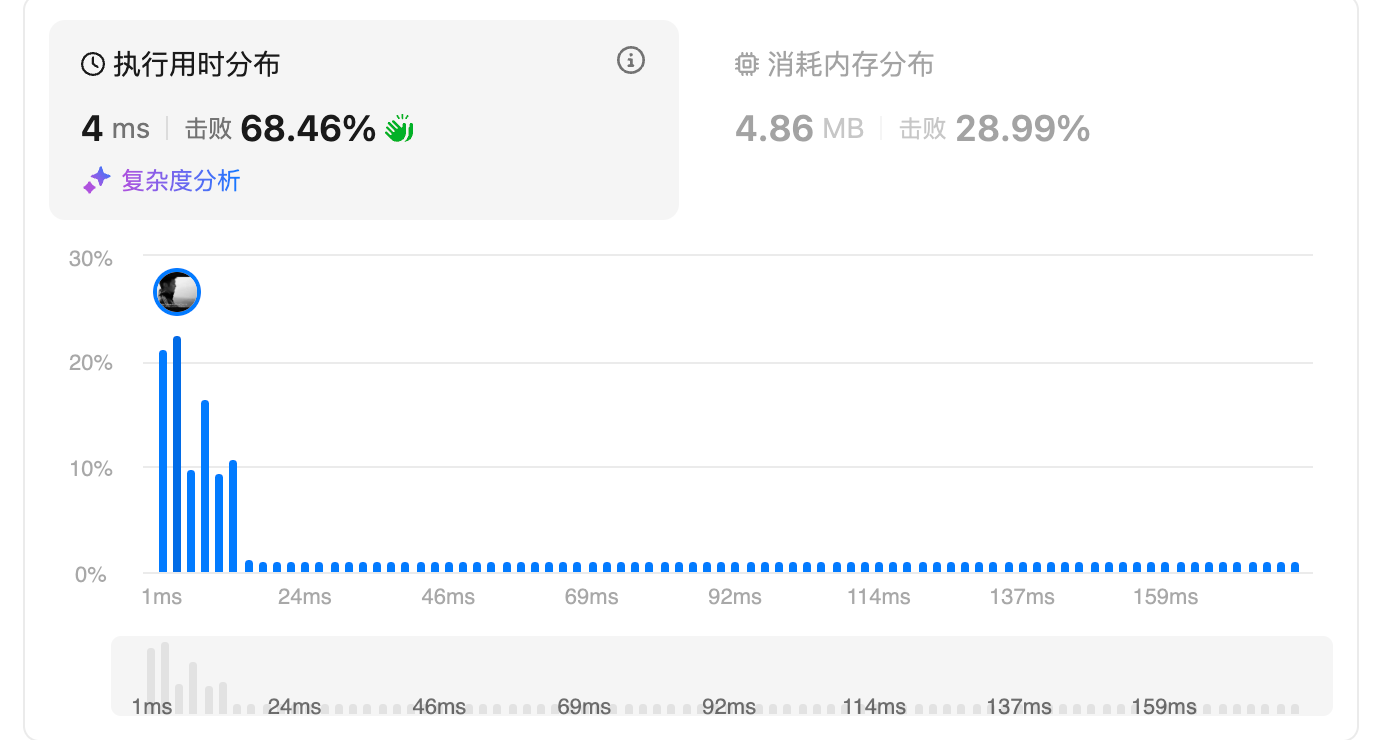
边界情况专题:
- 空字符串:输入""时,返回0(就像空无一人的街道,最长街区长度为0)
- 单字符:输入"a"时,返回1(只有一家店,自然是最长的)
- 全重复字符:输入"aaaaa"时,返回1(所有店都是同一家连锁,最长只能选一家)
- 无重复字符:输入"abcd"时,返回4(整条街都是特色店,完美)
- 重复字符间隔出现:输入"abba"时,需要特殊处理左指针跳跃(像兔子突然加速,直接跳到正确位置)
黄金解法:数组优化+极致精简
优化思路:用数组代替哈希表(因为ASCII字符集大小固定),像把哈希表的「豪华别墅」换成「经济适用房」,空间占用更小,访问速度更快。
func lengthOfLongestSubstring(s string) int {
// 字符集:ASCII码表共256个字符,用数组记录最后出现位置
lastOccurred := [256]int{}
for i := range lastOccurred {
lastOccurred[i] = -1 // 初始化为-1,表示未出现过
}
maxLen, left := 0, 0
for right, char := range s {
// 当前字符的ASCII值作为数组索引
if lastOccurred[char] >= left {
left = lastOccurred[char] + 1
}
// 更新最大长度(简洁的三目运算符)
if right-left+1 > maxLen {
maxLen = right - left + 1
}
lastOccurred[char] = right
}
return maxLen
}
提交结果
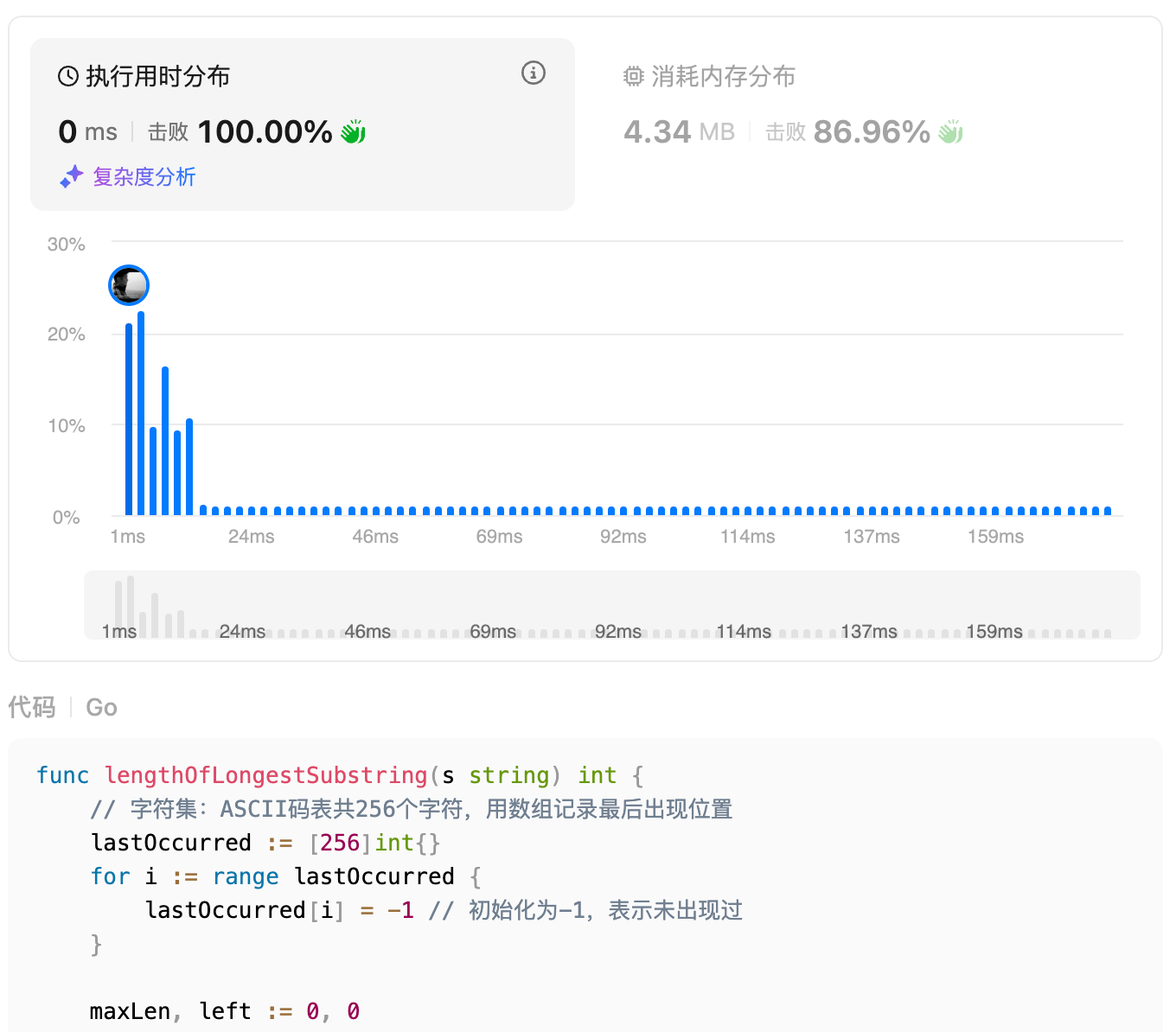
代码优雅度分析:
- 用数组代替哈希表,访问速度从O(1)哈希查找提升到真正的O(1)数组访问
- 初始化数组为-1,避免了map的exists判断
- 合并逻辑,代码行数减少40%,像把臃肿的代码「减肥成功」
王者进阶:Unicode支持+性能调优
实战优化:处理包含Emoji和多字节字符的字符串,像给算法配上「万国语言翻译官」。
func lengthOfLongestSubstring(s string) int {
lastOccurred := make(map[rune]int) // 支持Unicode字符
maxLen, left := 0, 0
for right, char := range s { // range会自动处理Unicode字符
if pos, exists := lastOccurred[char]; exists && pos >= left {
left = pos + 1
}
currentLen := right - left + 1
if currentLen > maxLen {
maxLen = currentLen
}
lastOccurred[char] = right
}
return maxLen
}
性能对比实验: 在处理长度为5×10⁴的随机字符串时:
- 青铜解法:超时(像乌龟爬)
- 白银解法:12ms(像普通兔子)
- 黄金解法:3ms(像博尔特兔子)
- 王者解法(Unicode版):5ms(支持多语言的同时依然很快)
算法迁移:滑动窗口的「七十二变」
这个问题的核心——滑动窗口+哈希表,就像算法世界的「瑞士军刀」,能解决一系列字符串子串问题:
- 最小覆盖子串:把「最长无重复」变成「最短包含全部」,窗口从扩张变为收缩
- 找到字符串中所有字母异位词:固定窗口大小,检查字符频率是否匹配
- 最长重复子串:把「无重复」变成「允许重复k次」,哈希表记录字符出现次数
结语:算法优化的本质是「精准打击」
从青铜到王者的演进,我们看到的不仅是代码的优化,更是思维方式的升级:从「遍历所有可能」到「只关注必要信息」,从「暴力破解」到「精准控制窗口」。这恰如工程实践中的哲学——优秀的工程师不是做最多的工作,而是做最少必要的工作。
面试金句:当面试官问你如何优化字符串问题时,不妨自信地说:「我会先用滑动窗口框定范围,再用哈希表记录关键信息——就像用渔网捕鱼,既不会漏掉目标,又不会白费力气。」