两数之和:从暴力到优雅的算法演进
引言:一道题看穿算法思维
让我猜猜,你是不是也曾在面试中遇到过这道题?作为LeetCode的开山第一题,两数之和不仅是算法入门的敲门砖,更是检验工程师思维方式的试金石。8年云原生开发经验告诉我:解决问题的代码大同小异,而优化问题的思路才是真正拉开差距的关键。今天GO兔就来扒开这道题的层层外衣,看看从青铜到王者的解法中藏着哪些算法智慧。
一、青铜解法:简单粗暴的双重循环
1.1 直观思路
最容易想到的解法就像在人群中找朋友——挨个问每个人:"你好,能和我凑成target吗?"。遍历数组中的每个元素,再检查它后面的元素是否能与之配对。
1.2 Go代码实现
func twoSum(nums []int, target int) []int {
for i := 0; i < len(nums); i++ {
for j := i + 1; j < len(nums); j++ {
if nums[i]+nums[j] == target {
return []int{i, j}
}
}
}
return nil // 题目保证有解,实际可省略
}
提交结果
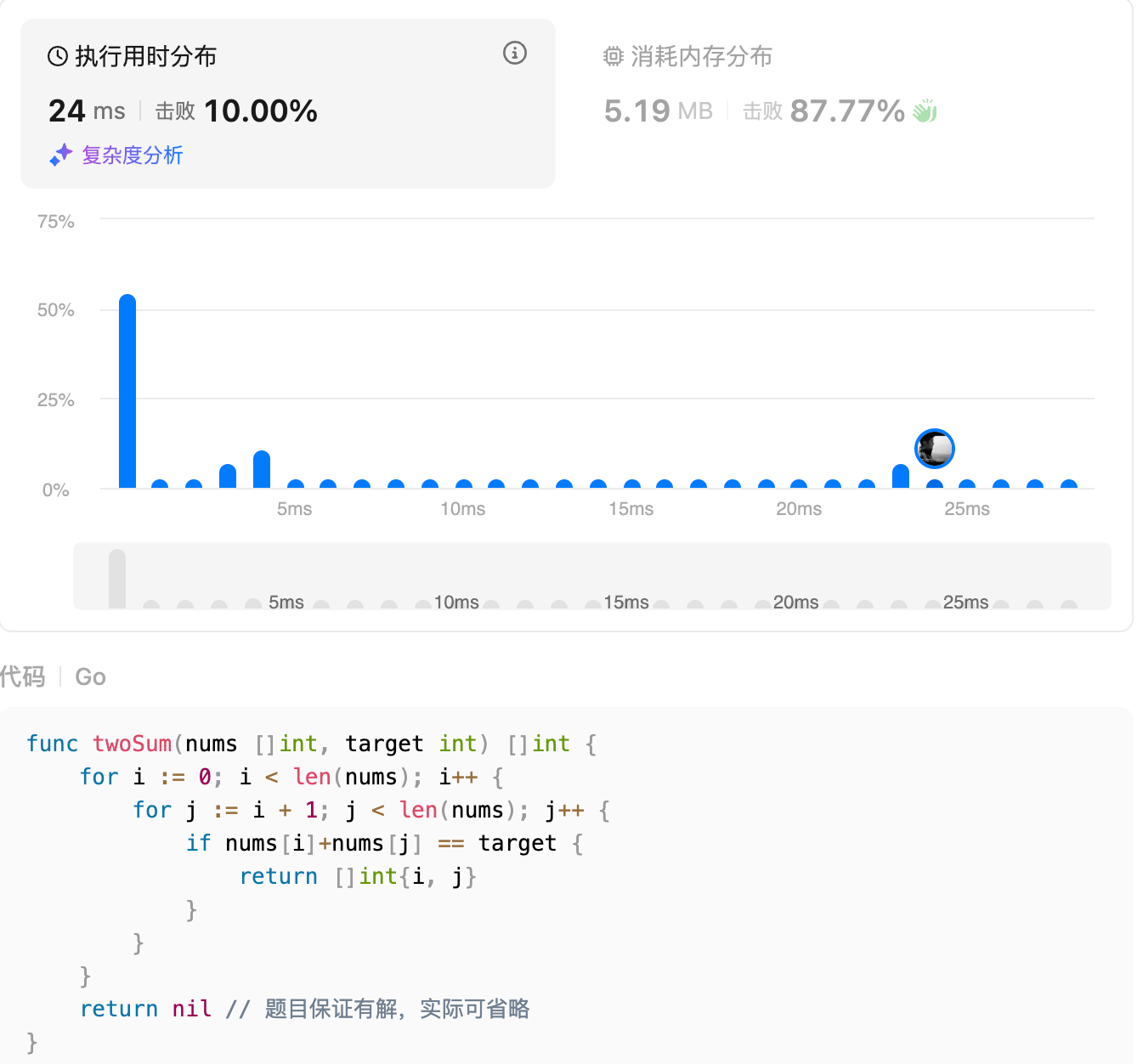
1.3 复杂度分析
- 时间复杂度:O(n²) - 双层循环就像嵌套的俄罗斯套娃,数据量翻倍时,工作量会变成原来的四倍
- 空间复杂度:O(1) - 不需要额外空间,堪称"空间洁癖患者福音"
1.4 致命缺陷
当数组长度超过10000时,这个解法就像蜗牛赛跑——在LeetCode上会直接超时。我曾见过有候选人在面试中写出这个解法后,被面试官追问:"如果这是生产环境的千万级数据,你打算让服务器跑多久?"
二、白银解法:排序+双指针的迷惑行为
2.1 看似聪明的思路
有些同学会想到:先排序,再用双指针从两端向中间逼近。这个思路在求"两数之和等于target"的数值时确实高效,但在本题中却暗藏陷阱。
2.2 问题所在
题目要求返回的是原始数组的下标,而排序会彻底打乱元素的位置信息。虽然可以通过结构体保存原始下标,但这会让代码复杂度飙升,得不偿失。
经典错误示范:某大厂面试现场,候选人花15分钟实现了排序+双指针解法,最后发现无法还原原始下标,场面一度十分尴尬。
三、黄金解法:哈希表的空间换时间魔法
3.1 核心洞察
我们需要一个"记忆助手",记住已经遍历过的数字及其下标。当遇到新数字时,只需问问这个助手:"target - 当前数字"是否在之前出现过?
3.2 Go代码实现
func twoSum(nums []int, target int) []int {
numMap := make(map[int]int)
for i, num := range nums {
complement := target - num
if j, ok := numMap[complement]; ok {
return []int{j, i}
}
numMap[num] = i
}
return nil
}
提交结果
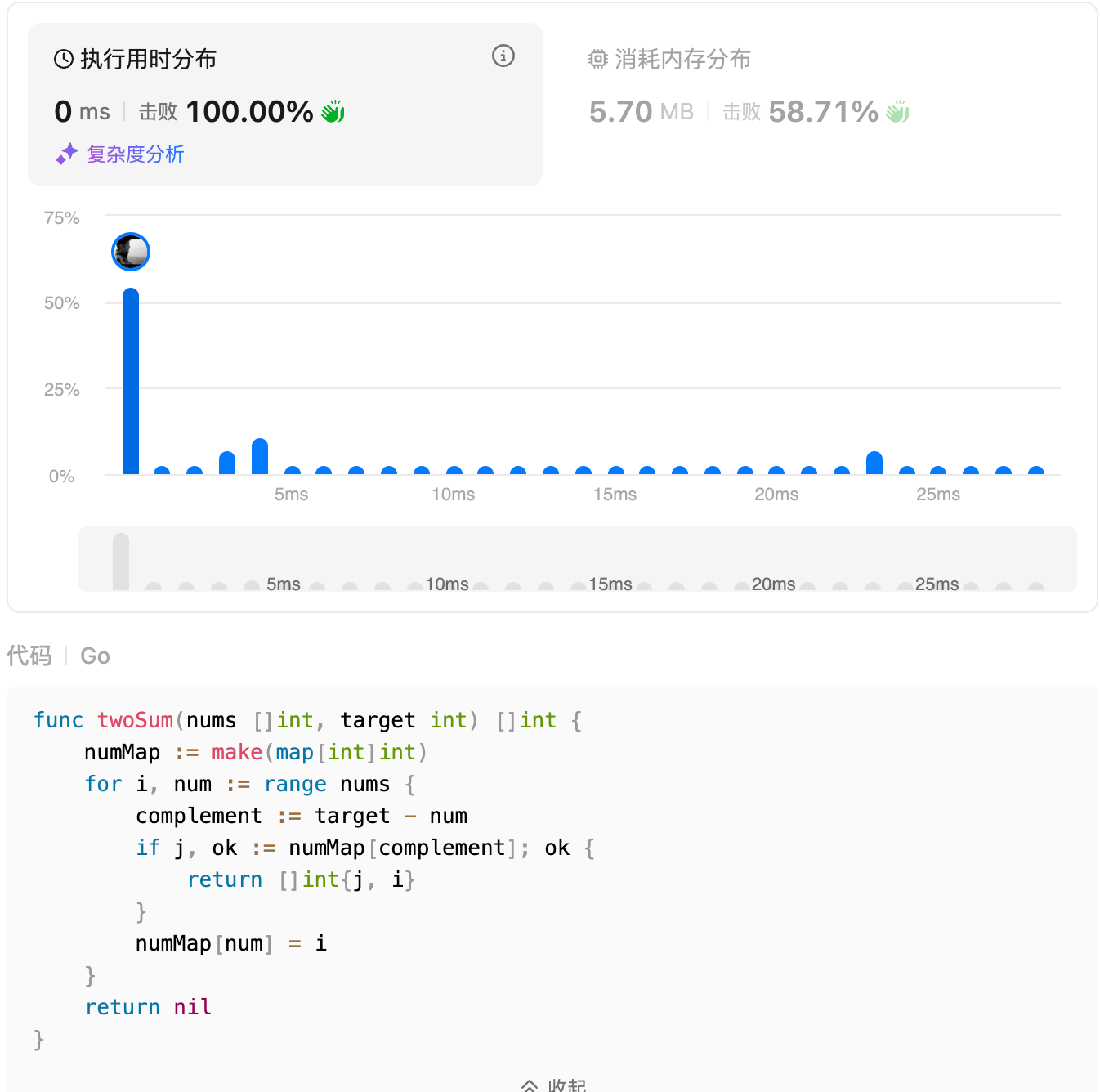
3.3 为什么这样高效?
- 时间复杂度:O(n) - 只需遍历一次数组,哈希表的查找操作平均是O(1)
- 空间复杂度:O(n) - 需要存储已遍历的元素,用空间换取了时间
3.4 Go语言的精妙细节
- map初始化:直接使用
make(map[int]int)而非make(map[int]int, len(nums))——Go的map会自动扩容,预设容量反而可能浪费空间 - 短路返回:一旦找到解立即返回,避免无效迭代
- 先查后存:确保不会重复使用同一个元素,完美规避
nums[i] * 2 == target的情况
四、王者进阶:实战中的边界情况处理
4.1 处理重复元素
// 测试用例: nums = [3,3], target = 6
// 正确输出: [0,1]
// 错误输出: [0,0] (如果先存后查)
先查询哈希表再存入当前元素,这个顺序是精髓所在!就像你不会在介绍自己之前就问别人是否认识你一样。
4.2 性能优化技巧
对于海量数据,可以预先分配map容量:
numMap := make(map[int]int, len(nums)) // 减少map动态扩容开销
4.3 并发安全考量
在Go的并发场景中,需要使用sync.Map替代普通map:
import "sync"
func twoSumConcurrent(nums []int, target int) []int {
var numMap sync.Map
for i, num := range nums {
complement := target - num
if j, ok := numMap.Load(complement); ok {
return []int{j.(int), i}
}
numMap.Store(num, i)
}
return nil
}
五、算法思维的迁移应用
两数之和的哈希表思想可以推广到更多场景:
- 三数之和:固定一个数,转化为两数之和问题
- 四数之和:固定两个数,转化为两数之和问题
- 子数组和等于K:前缀和+哈希表
面试金句:当面试官问你"还有更优解吗?"时,不妨反问:"您更关注时间效率还是空间效率?在我们的生产环境中,通常会选择..."
结语:算法优化的本质是 trade-off
从O(n²)到O(n)的演进,不仅是效率的提升,更是思维方式的转变。在云原生时代,这种权衡取舍的思想尤为重要——就像我们选择用内存换CPU时间,用缓存换响应速度。记住:最好的算法不是最复杂的,而是最适合当前场景的。
下一次遇到算法题时,不妨先问自己三个问题:
- 暴力解法是什么?(青铜思路)
- 时间瓶颈在哪里?(优化方向)
- 能用空间换时间吗?(哈希表思维)
这三个问题,或许能帮你打开算法世界的大门。